Relação entre a folha A4 e a raiz de 2

Às vezes eu digo que matemática é como a massa que fica entre os tijolos ou o ferro e concreto que estão ali em uma construção e que é importante para esta construção, mas que ninguém vê. O fato de você não vê uma aplicação imediata não quer dizer que ela não exista e hoje eu quero mostrar a vocês como a $\sqrt{2}$ está presente em sua vida e você, talvez, não saiba... ;-)

• Agenda planejador diário 2021-2022 Sokg
• Livros em oferta
  

Alguma vez você já parou para reparar nas dimensões da folha A4? Na verdade o que vamos falar aqui não funciona apenas para folhas A4. Também valem para A5, A3, A2, etc. Estas dimensões têm algo em comum. Se você dividir o lado maior pelo lado menor vai encontrar $\sqrt{2}$. Veja um exemplo de tamanho de folhas A4 como mostra na figura seguinte.

 

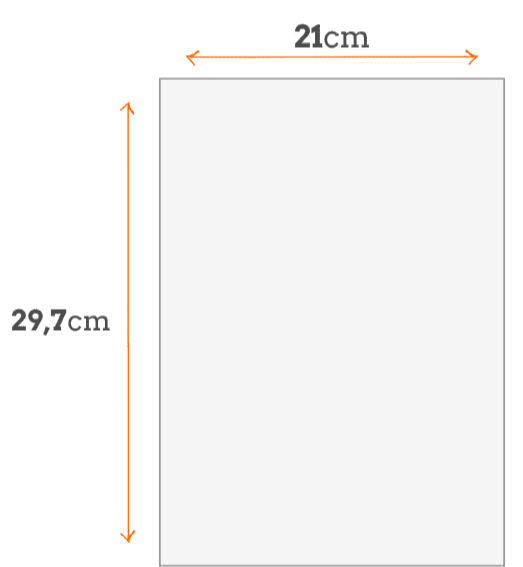
Se dividir 29,7 por 21 encontrará 1,414285714, que é um valor aproximado para $\sqrt{2}$. Se usar uma calculadora verá que 1,414213562 é o número obtido quando pede para calcular a $\sqrt{2}$ (que é uma aproximação para este número, pois, como é irracional, não pode ser escrito como um número decimal finito, mas podemos deixar esta discussão mais técnica para outro momento ;-)). 

 

A metade de uma folha A4 é uma miniatura da folha A4 original

O que acontece quando você dobra uma folha A4 no meio? Deverá ter algo como o mostrado na figura abaixo

Folha A4 dobrada ao meio uma vez

 

Talvez tenha lhe passado despercebido, mas se você olhar para uma folha A4 dobrada ao meio (a metade dela, portanto) é uma miniatura da folha A4 original, ou seja, ela mantém a proporção entre os lados. Em outras palavras, se dividir o lado maior pelo lado menor ainda continuará a encontrar 1,414285714. Se dividir novamente essa folha menor, que já é miniatura da folha A4, encontrará uma folha menor ainda que também será miniatura da maior.

Folha A4 dobrada ao meio duas vezes

 

Se pegar o lado maior do quarto da folha A4 e dividir pelo lado menor deste quarto obterá...... Isso mesmo 1,414285714 que é um valor aproximado para $\sqrt{2}$. 

 

Este livro apresenta o Cálculo com a possibilidade de estudo junto com dois softwares: GeoGebra e MAXIMA.

 

A matemática por trás do fenômeno

A matemática por trás dessa mágica de dividir ao meio e obter miniaturas da folha original é simples. Essas dimensões foram pensadas para ser assim. Qual deve ter sido a pergunta original quando se pensou em definir a proporção entre lado maior e lado menor? Penso que deve ter sido algo como "Queremos uma proporção entre lado maior e lado menor de tal modo que estas proporções se mantenham quando a folha for dobrada ao meio".

 

Bom, uma pessoa com um conhecimento básico de matemática (geralmente se estuda proporções no 7º ano?) deve ter feito um cálculo rápido mais ou menos como segue

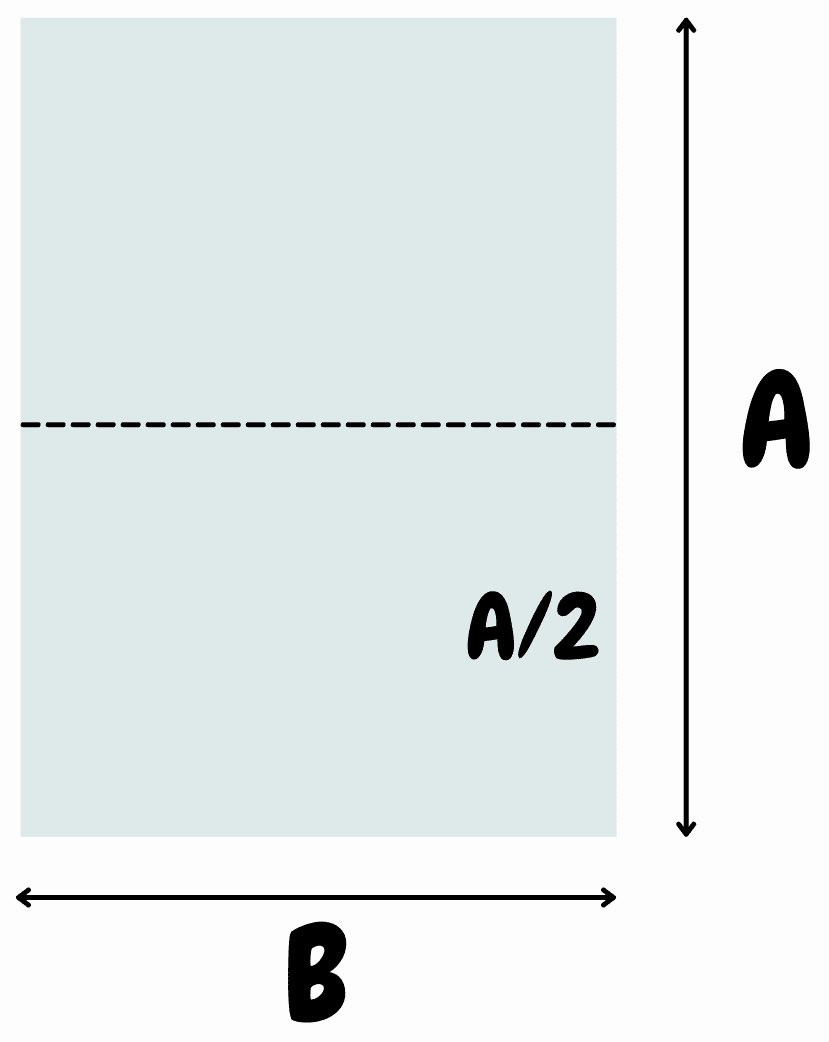
Lembre-se que a característica que se quer é que a razão entre Lado Maior e Lado Menor seja o mesmo, tanto para a folha inteira quando para a sua metade. Podemos escrever assim $$\frac{\mbox{Lado Maior da folha maior [A]}}{\mbox{Lado Menor da folha maior [B]}}=\frac{\mbox{Lado Maior da folha menor [B]}}{\mbox{Lado Menor da folha menor [A/2]}}.$$ Se isso acontecer teremos a proporção mantida e isso é o que chamamos no início deste texto como uma "miniatura". Se usarmos A para representar a Altura, B para representar a Base podemos "traduzir" para símbolos matemáticos da seguinte forma $$\frac{A}{B}=\frac{B}{A/2}.$$

Como estamos diante de uma proporção, então o produto cruzado deve dar o mesmo resultado, certo? [A fala correta seria: o produto dos meios deve ser igual ao produto dos extremos] e assim teremos $$\frac{A^2}{2}=B^2$$

Uma manipulação algébrica simples nos levará para $$\frac{A^2}{B^2}=2$$

de onde vem que $$\left(\frac{A}{B}\right)^2=2$$

Agora, extraindo a raiz quadrada em ambos os membros obtemos $$\frac{A}{B}=\sqrt{2}.$$

Ou seja, a razão entre a Altura e a Base deve ser... $\sqrt{2}$... Isso mesmo. ;-) Então, veja só... Você tem um número irracional presente quase todos os dias em sua vida e talvez não soubesse ainda...

Outros tamanhos de folhas

Quando você dobra uma folha A4, você encontra duas folhas menores, certo? Cada uma destas folhas é uma folha A5. Veja na ilustração abaixo

E se você dobrar uma folha A5 ao meio, você encontra uma folha A6 e assim por diante... Veja na imagem seguinte uma ilustração.

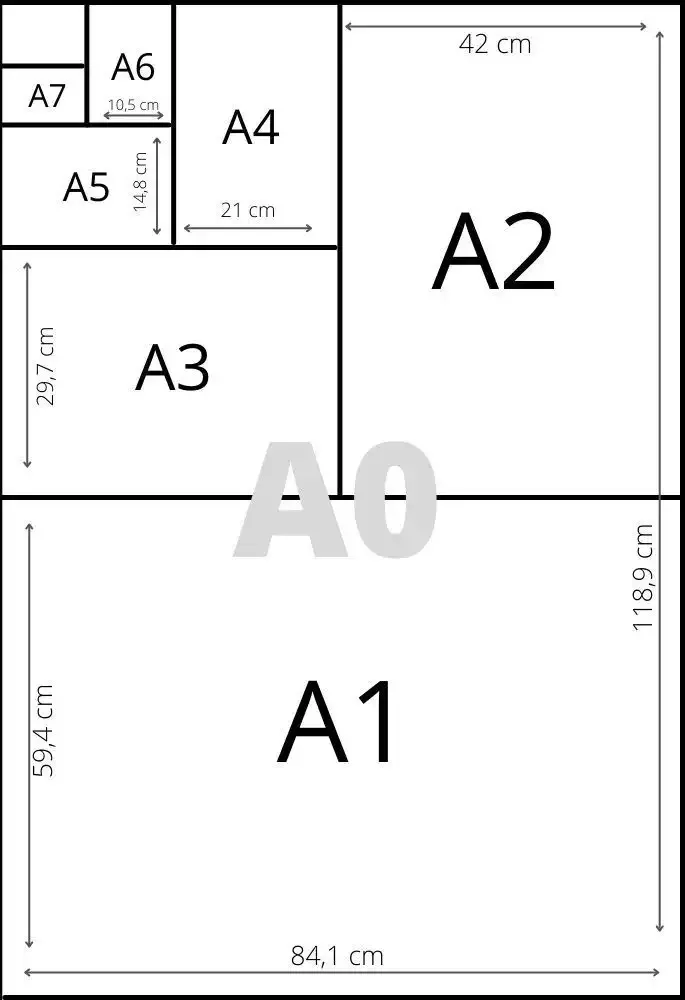
Seguindo esta lógica, como você encontra uma folha A3? Isso mesmo, colocando duas folhas A4 juntas e encontrará uma folha A2 colocando duas folhas A3 juntas e assim por diante... A imagem seguinte ilustra essas relações a partir do tamanho A0.

Fonte: https://www.significados.com.br/tamanho-de-folha/

 

Interessante, não? Se o tamanho fosse escolhido de uma forma aleatória, não haveria essas versões em miniatura das folhas maiores. Para que isso aconteça, a razão (divisão) entre as medidas do lado maior e do lado menor deve ser igual a $\sqrt{2}$. ;-)


Abração pro 6
Luís Cláudio LA