Quem nunca ouviu dizer que a Terra é achatada nos polos?
A Terra de fato é achatada nos polos, mas o desenhos como vemos AQUI (e livros estão cheio deles) dão a impressão de que esse oval (na verdade um elipsoide) é perceptível, mas com certeza, não é. Se olhar a Terra do espaço verá uma imagem semelhante a uma bola de bilhar. Tudo bem, trata-se de um exagero para fins didáticos, mas o problema é que, geralmente, não se chama muito a atenção para o fato de que na verdade a Terra é praticamente uma esfera e esse achatado não é possível ver, mesmo se estiver no espaço vendo todo o planeta.

Antes de prosseguir, uma rápida nota sobre o fato do raio ser maior no Equador em função da força centrífuga que o movimento de rotação da Terra produz e pode ser algo interessante de ser explorado pelo professor de Física e Geografia.
Um elipsoide que é praticamente uma esfera
A forma oval que nos referimos é chamada de Elipsoide. No caso da Terra é sabido que ela é um elipsoide com o raio polar (de 6.356,75 km) ao raio equatorial (6.378,1 km), que nos dá um diâmetro equatorial de 12,756,3 km e um diâmetro polar de 12.713,5 km. Como pode ver, de fato o raio polar é menor que o raio equatorial em 21 km. Isso mesmo, apenas 21,35 km de diferença, ou uma variação no diâmetro de 42,7 km. Isso é menos do que a distância de Brasília à Formosa ou Luziânia; menos que a distância de Goiânia até Anápolis.
O desenho seguinte foi feito com o software GeoGebra e é um elipsoide com as mesmas características da Terra, ou seja, raio equatorial e polar como descritos acima.
Ela é achatada nos polos, mas isso é visível como as imagens que vemos deixa parecer?
O desenho seguinte foi feito com o software GeoGebra e é um elipsoide com as mesmas características da Terra, ou seja, raio equatorial e polar como descritos acima.
Ela é achatada nos polos, mas isso é visível como as imagens que vemos deixa parecer?
Esse desenho acima está estático mas você pode movimentá-lo no GeoGebra se baixar ESSE APPLET CLICANDO AQUI. Segure o botão do lado direito do mouse e arraste-o para mudar a visualização. Ao girar a rodinha do mouse poderá aproximar ou distanciar do desenho.
Na imagem seguinte colocamos a Terra Real (vamos assim chamar) e a Terra Esférica considerando o raio equatorial como o raio da esfera.
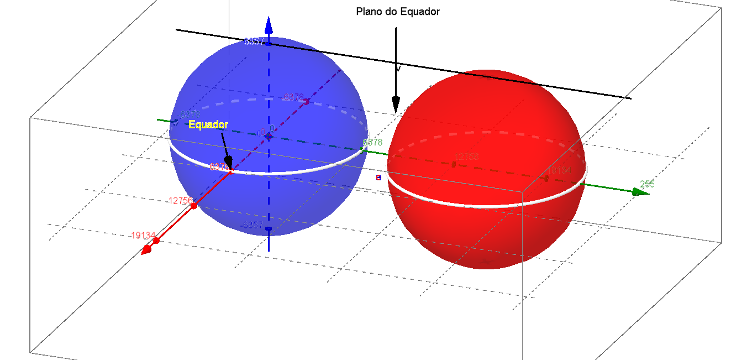
O azul é a representação real da Terra como um elipsoide de raio polar e equatorial como no texto e o vermelho é uma esfera com raio equatorial.

O azul é a representação real da Terra como um elipsoide de raio polar e equatorial como no texto e o vermelho é uma esfera com raio equatorial.
Interaja com ESTA CONSTRUÇÃO clicando e arrastando o mouse para mudar o ponto de vista.
E aí? Ainda acha que o "achatado nos polos" é visível?
O fabricante desta bola (Aramith) garante que a tolerância para o erro na medida do raio é de 0,001 polegada (cerca de 0,0254 mm pois em 1 polegada há 25,4 mm - regra de três simples). Então o erro no diâmetro é no máximo de 0,0508 mm. Essa bola tem um diâmetro oficial de 52,4 mm. Desse modo, o diâmetro dela é no mínimo 52,4 mm - 0,0508 mm = 52,3492 mm e no máximo 52,4 mm + 0,0508 mm = 52,4508 mm
A diferença entre o ponto mais distante o mais próximo do centro da bola de bilhar é R-r em que R é o raio maior e "r" o raio menor, ou seja,
$$R-r=\cfrac{52,4508}{2}-\cfrac{52,3492}{2}=\cfrac{0,1016}{2}=0,0508\,mm$$
Para compararmos a Terra com uma bola de bilhar teremos que fazer de duas, uma das alternativas a seguir. Aumentar a bola de bilhar até o tamanho da Terra ou diminuir a Terra até uma bola de bilhar. Vamos diminuir a bola de bilhar até o tamanho da Terra, proporcionalmente.
Vejamos, tomemos por base o diâmetro equatorial da Terra que mede 12.756,3 km. O diâmetro equatorial da bola de bilhar é 52,3492 mm. Precisamos estar com a mesma unidade de medida. Fazendo a conversão chegaremos que 12.756,3 km (o diâmetro equatorial da Terra) é o mesmo que 12.756.300.000 mm . Com isso em mente já temos como descobrir qual é o fator de escala.
$$52,3492 . x=12.756.300.000\Rightarrow x\approx 243.677.076,25$$
Assim, para trazermos a Terra para o tamanho de uma bola de bilhar precisamos dividir suas medidas por 243.677.076,25 (tomando por base o diâmetro equatorial).
Logo acima mostramos que a diferença entre o ponto mais distante do centro da bola de bilhar e o mais próximo é de apenas 0,0508 mm. Que número é esse em relação a Terra?
Sabemos que o pico mais alto da Terra é o Evereste que fica a 8.848 m de altitude e o mais baixo (para quem veria do espaço) fica no Mar Morto, na fronteira entre a Jordânia e Israel, com uma altitude de - 400 m (ou seja, 400 m abaixo do nível do mar). A diferença entre o ponto mais alto e o ponto mais baixo é, portanto, 8848-(-400)=8848+400=9248 m =9,248 km.
Trazendo esse número para a nossa escala da bola de bilhar teríamos:
$$\cfrac{9.248.000}{243.677.076,25}\approx 0,03795$$
Terra reduzida ao tamanho de uma bola de bilhar: diferença entre o ponto mais distante e o mais próximo do centro: 0,0378 mm.
Ou seja, na bola de bilhar há uma variação maior entre os pontos mais distantes e mais próximos do centro do que na Terra reduzida ao tamanho de uma bola de bilhar, ou seja,
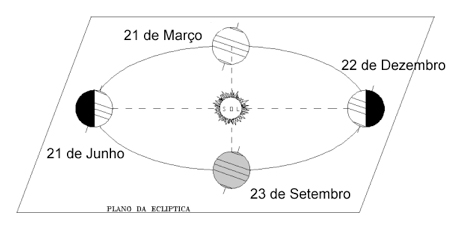
Fato semelhante ocorre em relação à órbita da Terra em torno do Sol? Ela dificilmente seria uma circunferência pois mesmo que fosse de 1 metro a distância entre os focos da elipse isso faria da órbita uma elipse e não uma circunferência. De fato é uma elipse, mas os focos são muito próximos um do outro, ou seja, a excentricidade desta elipsed é praticamente zero (calcule :-)) e assim como o formato de esfera da Terra, a órbita de nosso planeta é uma elipse praticamente circunferência. O desenho geralmente é feito em uma perspectiva de visão como se estivéssemos vendo um a órbita não de cima para baixo, mas em outra posição.
Ocorre que geralmente não é chamado a atenção para isso, como se vê no desenho a seguir em que o autor tomou o cuidado de colocar o desenho em um plano (quase) horizontal.
A Terra é mais lisa do que uma bola de bilhar
Suponha que você esteja em uma posição em que possa ver toda a Terra em seu campo de visão. Afirmo que você verá ao que é mais esférico que uma bola de bilharO fabricante desta bola (Aramith) garante que a tolerância para o erro na medida do raio é de 0,001 polegada (cerca de 0,0254 mm pois em 1 polegada há 25,4 mm - regra de três simples). Então o erro no diâmetro é no máximo de 0,0508 mm. Essa bola tem um diâmetro oficial de 52,4 mm. Desse modo, o diâmetro dela é no mínimo 52,4 mm - 0,0508 mm = 52,3492 mm e no máximo 52,4 mm + 0,0508 mm = 52,4508 mm
A diferença entre o ponto mais distante o mais próximo do centro da bola de bilhar é R-r em que R é o raio maior e "r" o raio menor, ou seja,
$$R-r=\cfrac{52,4508}{2}-\cfrac{52,3492}{2}=\cfrac{0,1016}{2}=0,0508\,mm$$
Para compararmos a Terra com uma bola de bilhar teremos que fazer de duas, uma das alternativas a seguir. Aumentar a bola de bilhar até o tamanho da Terra ou diminuir a Terra até uma bola de bilhar. Vamos diminuir a bola de bilhar até o tamanho da Terra, proporcionalmente.
Vejamos, tomemos por base o diâmetro equatorial da Terra que mede 12.756,3 km. O diâmetro equatorial da bola de bilhar é 52,3492 mm. Precisamos estar com a mesma unidade de medida. Fazendo a conversão chegaremos que 12.756,3 km (o diâmetro equatorial da Terra) é o mesmo que 12.756.300.000 mm . Com isso em mente já temos como descobrir qual é o fator de escala.
$$52,3492 . x=12.756.300.000\Rightarrow x\approx 243.677.076,25$$
Assim, para trazermos a Terra para o tamanho de uma bola de bilhar precisamos dividir suas medidas por 243.677.076,25 (tomando por base o diâmetro equatorial).
Logo acima mostramos que a diferença entre o ponto mais distante do centro da bola de bilhar e o mais próximo é de apenas 0,0508 mm. Que número é esse em relação a Terra?
Sabemos que o pico mais alto da Terra é o Evereste que fica a 8.848 m de altitude e o mais baixo (para quem veria do espaço) fica no Mar Morto, na fronteira entre a Jordânia e Israel, com uma altitude de - 400 m (ou seja, 400 m abaixo do nível do mar). A diferença entre o ponto mais alto e o ponto mais baixo é, portanto, 8848-(-400)=8848+400=9248 m =9,248 km.
Trazendo esse número para a nossa escala da bola de bilhar teríamos:
$$\cfrac{9.248.000}{243.677.076,25}\approx 0,03795$$
Conclusão
Bola de Bilhar: diferença entre o ponto mais distante e o mais próximo do centro: 0,0508 mm.Terra reduzida ao tamanho de uma bola de bilhar: diferença entre o ponto mais distante e o mais próximo do centro: 0,0378 mm.
Ou seja, na bola de bilhar há uma variação maior entre os pontos mais distantes e mais próximos do centro do que na Terra reduzida ao tamanho de uma bola de bilhar, ou seja,
A TERRA É MAIS LISA DO QUE UMA BOLA DE BILHAR.
Em tempo: encontrei um vídeo no YouTube do canal Primata Falante em que o Davi Simões fala mais sobre esse assunto com um olhar um pouco mais amplo. Vale a pena conferir. Além da comparação com a bola de bilhar ele ainda mostra outros motivos pelo qual a forma da Terra tem esse formato esférico (e uma esfera quase perfeita) :-)
---
Nada contra os elipsoides. :-) Olha que beleza esta construção mostrada na figura seguinte na forma de um elipsoide, mas... Esse não é o formato da Terra que se percebe a olho nu.
---
Nada contra os elipsoides. :-) Olha que beleza esta construção mostrada na figura seguinte na forma de um elipsoide, mas... Esse não é o formato da Terra que se percebe a olho nu.
 |
| Infosys, Pune |
EM TEMPO
Órbita da Terra ao redor do SolFato semelhante ocorre em relação à órbita da Terra em torno do Sol? Ela dificilmente seria uma circunferência pois mesmo que fosse de 1 metro a distância entre os focos da elipse isso faria da órbita uma elipse e não uma circunferência. De fato é uma elipse, mas os focos são muito próximos um do outro, ou seja, a excentricidade desta elipsed é praticamente zero (calcule :-)) e assim como o formato de esfera da Terra, a órbita de nosso planeta é uma elipse praticamente circunferência. O desenho geralmente é feito em uma perspectiva de visão como se estivéssemos vendo um a órbita não de cima para baixo, mas em outra posição.
Ocorre que geralmente não é chamado a atenção para isso, como se vê no desenho a seguir em que o autor tomou o cuidado de colocar o desenho em um plano (quase) horizontal.
Um rápido comentário aos estudantes
Nesta postagem foram usados vários conceitos que geralmente são estudados no Ensino Fundamental (basicamente). Muitos sempre questionam: por que tenho que estudar isso? Onde utilizo isso em minha vida cotidiana? A matemática da vida cotidiana é aquela que vai até a antiga 6ª série (7º ano hoje). É lá onde se aprende regra de três, porcentagem, juro simples, juro composto, resolver equações de 1º grau, conversão de medidas etc. Se você leu com atenção viu que usamos quase tudo isso aqui.- Básico de circunferência e esfera: relação entre raio e diâmetro.
- Conversão de medidas: quando transformamos 12.756,3 km em 12.756.300.000 mm.
- Regra de Três Simples: quando transformamos 0,001 polegadas em 0,0254 mm.
- Fator de escala: quando trouxemos a Terra para o tamanho de uma bola de bilhar.
- Números inteiros e operações: quando calculamos a diferença das altitudes do pico Evereste e o Mar Morto.
- Elipse: falamos rapidamente sobre elipse, foco e excentricidade. Geralmente é estudada no Ensino Médio (3ª série).
Na escola esses assuntos são vistos. Talvez o que falte é costurar esses retalhos para formar uma colcha de retalhos. :-)
A+ : Parametrizações para o GeoGebra
É importante saber escrever algumas parametrizações caso queira construir o desenho de algumas superfícies. O GeoGebra possui um comando para gerar superfícies 3D a partir de parametrizações. Sendo assim, caso queira construir alguns tipos de superfícies, é necessário que saiba lidar com as parametrizações. Geralmente estudamos sobre isso em disciplinas como Cálculo 2 ou 3 e Geometria Diferencial.
No caso do elipoide para a Terra Real (levando em conta o raio equatorial e o raio polar) fizemos o seguinte.
1) Criei as variáveis rp (para raio polar) e re (para raio equatorial) com os valores 6.357 e 6.378. Para isto basta entrar no CAMPO DE ENTRADA com rp=6357 (aperte ENTER) e re=6378 (aperte enter).
2) Uma parametrização para a elipse $\cfrac{x^2}{a^2}+\cfrac{x^2}{b^2}+\cfrac{z^2}{c^2}=1$ é $x=a.\sin(\phi).\cos(\theta)$, $y=b.\sin(\phi).\sin(\theta)$ e $z=c.\cos(\phi)$. Note que $x, y$ e $z$ satisfazem a equação do elipsoide.
3) Sabendo que o comando de entrada no GeoGebra tem a forma
Superfície[ <Expressão>, <Expressão>, <Expressão>, <Variável 1>, <Valor Inicial>, <Valor Final>, <Variável 2>, <Valor Inicial>, <Valor Final> ]
não é difícil perceber que a parametrização para produzir a Terra Real será
Superfície[re*sen(phi)*cos(theta), re*sen(phi)*sen(theta), rp*cos(phi), phi, 0, pi, theta, 0, 2*pi]
Para a Terra Esférica eu só desloquei o "y" 15.000 unidades para a direita ficando com
Foi desse modo que o desenho dos elipsoides e esfera (que estão no apontados acima) foram construídos usando parametrização de superfície.
E a Terra? Tem possibilidade de ela ser plana?
NÃO. Veja vários argumentos no livro seguinte. Deixamos como sugestão de leitura.
Um grande abraço
Luís Cláudio LA










Postar um comentário